拿破仑定理

编辑讨论上传视频拿破仑定理是法国著名的军事家拿破仑·波拿巴已知最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆中心恰为另一个等边三角形的顶点。”该等边三角形称为拿破仑三角形。如果向内（原三角形不需为等边三角形）作三角形，结论同样成立。^[1]中文名拿破仑定理外文名Napoleon’s Theorem别称拿破仑三角形提出者拿破仑·波拿巴提出时间1795年应用学科数学、欧几里得几何适用领域范围数学、教学适用领域范围欧式几何

验证推导

编辑在△ABC的各边上向外各作等边△ABF，等边△ACD，等边△BCE。如何证明：这3个等边三角形的外接圆共点？思路1：利用四点共圆来证明三圆共点。这是证明拿破仑定理的基础。证明：设等边△ABF的外接圆和等边△ACD的外接圆相交于O；连AO、CO、BO。∴ ∠AFB=∠ADC=60°；∵ A、F、B、O四点共圆；A、D、C、O四点共圆；∴ ∠AOB=∠AOC=120°；∴ ∠BOC=120°；∵ △BCE是等边三角形∴ ∠BEC=60°；∴ B、E、C、O四点共圆∴ 这3个等边三角形的外接圆共点。结论：因为周角等于360°，所以，∠AOB=∠AOC=120°时，∠BOC就等于120°；用四点共圆的性质定理和判定定理来证明三圆共点的问题。拿破仑定理证明图以任意三角形的三边为边向外作等边三角形，则这三个等边三角形的中心的连线是一个等边三角形。求证：上面3个等边三角形的中心M、N、P的连线构成一个等边三角形？

证明一

编辑思路1：利用已有的三个圆和三个四点共圆来证明。证明：设等边△ABD的外接圆⊙N，等边△ACF的外接圆⊙M，等边△BCE的外接圆⊙P相交于O；连AO、CO、BO。∵ A、D、B、O四点共圆；A、F、C、O四点共圆B、E、C、O四点共圆∠AFC=∠ADB=∠BEC=60°；∴ ∠AOB=∠AOC=∠BOC=120°；∵ NP、MP、MN是连心线；BO、CO、AO是公共弦；∴ BO⊥NP于X；CO⊥MP于Y；AO⊥NM于Z。∴ X、P、Y、O四点共圆；Y、M、Z、O四点共圆；Z、N、X、O四点共圆；∴ ∠N=∠M=∠P=60°；即△MNP是等边三角形。

证明二

编辑思路2：证明原三角形重心至外围三个等边三角形几何中心距离相等。

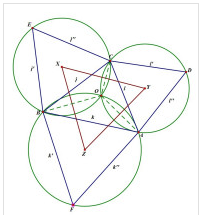
左图中绿色辅助线利用中线特性求其长度，绿色角度值亦可用余弦定理求出，结合垂角，进一步利用余弦定理求出两几何中心距离，同理可证原重心与另外两个等边三角形的几何中心距离。费马点也是证明拿破仑定理的好方法。拿破仑三角形证明方法二右图即是用费马点的性质来推导拿破仑定理的证明方法。

证明三

编辑思路3：用相似证明三边相等证明：如图，分别以△ABC的边BC、AC、AB为等边三角形边长，向△ABC外作等边三角形（△BCC’、△ACA’、△ABB’），设这三个三角形的中心分别为D，E，F，
　　则：∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30°
　　以点A为圆心，以AF长为半径作弧；以点E为圆心，以DC长为半径作弧。设两弧在多边形AFBDCE内交于点G。则AG=AF，GE=DC。
　　连接GF、GA、GE，DE、DF、EF。
　　∵△ABF、△BCD、△ACE都是底角为30°的等腰三角形（即∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30°）
　　∴△ABF∽△BCD∽△ACE，
　　∴AF/AB = AE/AC = DC/BC拿破仑三角形证明方法三　又∵AG=AF，GE=DC
　　∴AG/AB = AE/AC = GE/BC
　　∴△AGE∽△ABC
　　∴∠GAE=∠BAC
　　∴∠FAG = ∠EAF-∠GAE = ∠EAF-∠BAC = ∠FAB+∠EAC = 60°
　　又∵AG=AF
　　∴△AGF为等边三角形
　　∴AG=AF，∠AGF=60°　∵△AGE∽△ABC
　　∴∠AGE=∠ABC
　　又∵∠FBD = ∠ABC+∠FBA+∠DBC = ∠ABC+60°
　　∠FGE = ∠AGE+∠AGF = ∠AGE+60°
　　∴∠FBD=∠FGE
　　∵在△FBD和△FGE中，
　　FB=FG，∠FBD=∠FGE，BD=GE
　　∴△FBD≌△FGE(SAS)
　　∴FD=FE
　　同理，FD=DE
　　∵FD=DE=FE
　　∴△DEF为等边三角形

カテゴリー: 拿破仑定理