蝴蝶定理

编辑讨论上传视频蝴蝶定理（Butterfly Theorem），是古代欧氏平面几何中最精彩的结果之一。这个命题最早出现在1815年，由W.G.霍纳提出证明。而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号，题目的图形像一只蝴蝶。这个定理的证法不胜枚举，至今仍然被数学爱好者研究，在考试中时有各种变形。中文名蝴蝶定理外文名Butterfly Theorem别    称蝴蝶原理表达式XM=MY提出者W.G.霍纳提出时间1815年应用学科科学，数学，物理等适用领域范围理科，几何适用领域范围高等数学 验证推导霍纳证法等

目录

1. 1 定理定义
2. 2 验证推导
3. ▪ 霍纳证法
4. ▪ 作图法
5. ▪ 对称法
6. ▪ 面积法

1. ▪ 帕斯卡证法
2. ▪ 射影法
3. 3 定理推广
4. ▪ 1.蝴蝶定理的圆外形式：
5. ▪ 2.在圆锥曲线中：

1. ▪ 3.在筝形中
2. ▪ 4.坎迪定理
3. 4 发展历史
4. 5 定理意义

定理定义

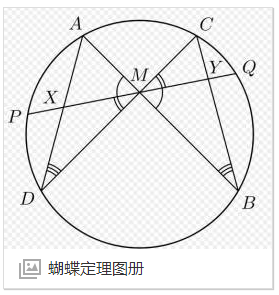
编辑蝴蝶定理（Butterfly Theorem）：设M为圆内弦PQ的中点，过M作弦AB和CD。设AD和BC各相交PQ于点X和Y，则M是XY的中点。
蝴蝶定理的证明该定理实际上是射影几何中一个定理的特殊情况，有多种推广（详见定理推广）：1. M作为圆内弦的交点是不必要的，可以移到圆外。2. 圆可以改为任意圆锥曲线。3. 将圆变为一个筝形，M为对角线交点。4. 去掉中点的条件，结论变为一个一般关于有向线段的比例式，称为“坎迪定理”， 不为中点时满足:

 ，这对1, 2均成立。^[1-2]

验证推导

编辑

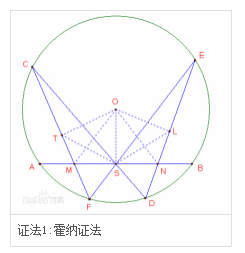
霍纳证法

过O作OL⊥ED，OT⊥CF，垂足为L、T，连接ON，OM，OS，SL，ST，易证明△ESD∽△CSF证法1:霍纳证法∴DS/FS=DE/FC根据垂径定理得：DL=DE/2，FT=FC/2∴DS/FS=DL/FT又∵∠D=∠F∴△DSL∽△FST∴∠SLD=∠STF即∠SLN=∠STM∵S是AB的中点所以OS⊥AB∴∠OSN=∠OLN=90°∴O，S，N，L四点共圆，同理，O，T，M，S四点共圆∴∠STM=∠SOM，∠SLN=∠SON∴∠SON=∠SOM∵OS⊥AB∴MS=NS

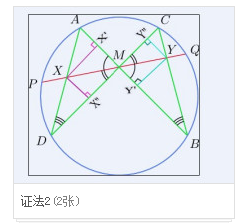
作图法

从X向AM和DM作垂线，设垂足分别为X’和X”。类似地，从Y向BM和CM作垂线，设垂足分别为Y’和Y”。证法2(2张)（证明过程见图片）证明方法二

对称法

（证明过程见图片）证法3:对称证法

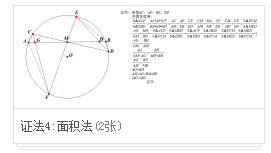
面积法

（证明过程见图片）【此方法也可证明蝴蝶定理的一般形式：坎迪定理】证法4:面积法(2张)

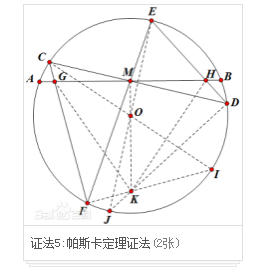
帕斯卡证法

连接CO、EO并延长分别交圆O于I、J，连接IF、DJ交于K，连接GK、HK。由帕斯卡定理得：M、O、K共线证法5:帕斯卡定理证法(2张)∵M为AB中点 ∴KM⊥AB∴∠GMK=∠HMK=90°又∵CI、EJ为⊙O直径∴∠GFK=∠HDK=90°又∵∠GMK=∠HMK=90°∴∠GMK+∠GFK=∠HMK+∠HDK=90°+90°=180°∴G、F、K、M共圆，H、D、K、M共圆∴∠GKM=∠GFM，∠MKH=∠MDH又∵∠GFM=∠MDH∴∠GKM=∠MKH又∵∠GMK=∠HMK=90°∴△GMK≡△HMK（ASA）∴GM=MH

射影法

1.构造特殊情况：如右图1，A’B’、C’D’、M’N’为⊙O’内三条直径，A’D’∩M’N’=P’，B’C’∩M’N’=Q’，则由圆中心对称性知P’O’=Q’O’.2.中心投影：在不属于⊙O’所在平面的空间上任取一点T作为投影中心，用平行于直线M’N’的平面截影，则圆O’被射影为椭圆，线段M’N’被射影为与之平行的M”N”，如图2，则对应存在P”O”=Q”O”.3.仿射：将图2的椭圆仿射为圆，如图3，由仿射不变性知PO=QO.

定理推广

编辑该定理实际上是射影几何中一个定理的特殊情况，有多种推广：

1.蝴蝶定理的圆外形式：

圆外蝴蝶定理如图，延长圆O中两条弦AB与CD交于一点M，过点M做OM垂线，垂线与CB和AD的延长线交于E、F，则可得出ME=MF（证明方法可参考蝴蝶定理的证法2、3、4）

2.在圆锥曲线中：

通过射影几何，我们可以非常容易的将蝴蝶定理推广到普通的任意圆锥曲线（包括椭圆，双曲线，抛物线，甚至退化到两条相交直线的情况）。圆锥曲线C上弦PQ的中点为M，过点M任作两弦AB，CD，弦AD与BC分别交PQ于X，Y，则M为XY之中点。而通过投影变换可以非常容易证明这个定理。射影几何里面关于投影变换有一个重要结论，对于平面上任意两个圆锥曲线C1,C2.任意指定C1内部一个点A1和C1上面一个点B1,另外任意指定C2内部一个点A2和C2上面一个点B2,存在唯一一个投影变换将曲线C1变换到C2而且A1变换到A2,B1变换到B2.由此对于本题，我们可以通过投影变换将C1变换成一个圆M，而将弦PQ的中点M变换成这个圆的圆心。在此变换以后，弦AB和CD都是圆M的直径而且四边形ACBD是圆M内接矩形，PQ也是一条直径，由对称性显然得出投影变换后M为X,Y的中点。又因为变换前后M都是线段PQ的中点，我们可以得出在直线PQ上这个变换是仿射变换，所以变换前M也是XY的中点。例题：椭圆中的蝴蝶定理如图一，椭圆的长轴A₁、A₂与x轴平行，短轴B₁B₂在y轴上，中心为M(o，r)（b>r>0）。（I）写出椭圆的方程，求椭圆的焦点坐标及离心率（II）直线y=k₁x交椭圆于两点C（x₁,y₁）,D(x₂，y₂)（y₂>0）；直线y=k₂x交椭圆于两点G（x₃，y₃），H（x₄，y₄）（y₄>0）。求证：k₁x₁x₂/(x₁+x₂)=k₂x₃x₄/(x₃+x₄)（III）对于（Ⅱ）中的C，D，G，H，设CH交X轴于点P，GD交X轴于点Q。求证： | OP | = | OQ |。（证明过程不考虑CH或GD垂直于X轴的情形）从x向AM和DM作垂线，设垂足分别为X’和X”。类似地，从Y向BM和CM作垂线，设垂足分别为Y’和Y’设：k1x1x2/(x1+x2)=k2x3x4/(x3+证明过程图片x4)为①式，两边同取倒数，得为1/k1x2+1/k1x1=1/k2x4+1/k2x3 ①’设：x1x4/(k1x1-k2x4)=-x2x3/(k1x2-k2x3)为 ②式，两边同取倒数，得k1/x4-k2/x1=k2/x2-k1/x3，移项得k2/x1+k2/x2=k1/x3+k1/x4 ②’将①’两边同乘以k1·k2，即得k2/x1+k2/x2=k1/x3+k1/x4它与②’完全一样。这里利用两式同时变形的方法可以较容易实现目的，有分析、有综合，有思维，有运算。思路的选择有赖于对式子特征的观察联想。纵观这道题的题目特征及解答过程，我们看到了用代数方程方法处理几何问题的作用与威力。

3.在筝形中

筝形中命题证明在筝形ABCD中，AB=AD，BC=CD，过直线BD上一点P任作两条直线，一条与直线 AD、BC 交于E、F，另一条与直线 AB、CD 分别交于 G、H，直线 GF、EH 分别与 BD 交于 I、J。则

特别地，当点 P 为 BD 中点时，有 PI=PJ。此时本题为1990年中国中学生数学冬令营选拔考试试题，被称为筝形蝴蝶定理。证明如图。 ^[3]

4.坎迪定理

去掉中点的条件，结论变为一个一般关于向量的比例式，成为「坎迪定理」，这对2，3均成立 ^[1]坎迪定理

发展历史

编辑这个命题最早作为一个征解问题出现于公元1815年英国的一本杂志《男士日记》（Gentleman’s Diary）39-40页（P39-40）上。有意思的是，直到1972年以前，人们的证明都并非初等，且十分繁琐。这篇文章登出的当年，英国一个自学成才的中学数学教师W.G.霍纳（他发明了多项式方程近似根的霍纳法）给出了第一个证明，完全是初等的；另一个证明由理查德·泰勒（Richard Taylor）给出。另外一种早期的证明由M.布兰德（Mile Brand）1827年的一书中给出。最为简洁的证法是射影几何的证法，由英国的J·开世在”A Sequel to the First Six Books of the Elements of Euclid”给出，只有一句话，用的是线束的交比。“蝴蝶定理”这个名称最早出现于《美国数学月刊》1944年2月号，题目的图形象一只蝴蝶。1981年，Crux杂志刊登了K.萨蒂亚纳拉亚纳（Kesirajn Satyanarayana）用解析几何的一种比较简单的方法，利用直线束，二次曲线束。 ^[1-2]1990年，CMO出现了筝形蝴蝶定理。 ^[4]

定理意义

编辑蝴蝶定理是古典欧式平面几何的最精彩的结果之一。这个定理的证法不胜枚举，至今仍然被数学热爱者研究，在考试中时有出现各种变形。 ^[1-2]词条图册更多图册词条图片(12)证法2(2)证法4:面积法(2)证法5:帕斯卡定…(2)1/2

数学定理

A-F

▪ 15定理	▪ 2π定理	▪ Sun-Ni定理	▪ Vizing定理
▪ 阿贝尔定理	▪ 阿贝尔二项式定理	▪ 阿贝尔-鲁菲尼定理	▪ 阿贝尔曲线定理
▪ 阿达马三圆定理	▪ 阿蒂亚-辛格指标定理	▪ 阿尔泽拉-阿斯科利定理	▪ 阿基米德原理
▪ 阿基米德中点定理	▪ 埃尔布朗定理	▪ 艾森斯坦定理	▪ 安达尔定理
▪ 奥尔定理	▪ 巴拿赫不动点定理	▪ 巴拿赫-塔斯基悖论	▪ 贝尔纲定理
▪ 贝亚蒂定理	▪ 贝叶斯定理	▪ 贝祖定理	▪ 本迪克森-杜拉克定理
▪ 本原元定理	▪ 闭图像定理	▪ 波尔查诺-魏尔斯特拉斯定理	▪ 伯恩斯坦定理
▪ 伯特兰-切比雪夫定理	▪ 博苏克-乌拉姆定理	▪ 博特周期性定理	▪ 不动点定理
▪ 布尔素理想定理	▪ 布朗定理	▪ 布劳威尔不动点定理	▪ 布列安桑定理
▪ 采样定理	▪ 陈氏定理	▪ 垂径定理	▪ 达布中值定理
▪ 大数定律	▪ 代数基本定理	▪ 单调收敛定理	▪ 单值化定理
▪ 等周定理	▪ 狄利克雷定理	▪ 迪尼定理	▪ 笛卡儿定理
▪ 笛卡儿符号法则	▪ 笛沙格定理	▪ 棣莫弗定理	▪ 棣莫弗-拉普拉斯定理
▪ 多项式定理	▪ 多项式余数定理	▪ 二次互反律	▪ 二项式定理
▪ 法图引理	▪ 法伊特-汤普森定理	▪ 凡·奥贝尔定理	▪ 反函数定理
▪ 范德瓦尔登定理	▪ 费马大定理	▪ 费马多边形数定理	▪ 费马平方和定理
▪ 费马小定理	▪ 芬斯勒-哈德维格尔定理	▪ 弗罗贝尼乌斯定理	▪ 辐角原理